一种高效而简单的FM解调方法

本文由基于LaTex的MathJax数学公式显示支持，加载可能需要一定时间。

测量复正弦信号瞬时频率的一种常用技术是计算信号瞬时$\theta(n)$相位的导数，如下图所示。

这是传统的离散信号FM解调方法，效果很好。解调器的瞬时输出频率为:

$$f(n)=\frac{f_s[∆\theta_{rad}(n)]}{2\pi}$$

其中$f_s$是以$Hz$为单位的采样率。

计算瞬时相位$\theta(n)$需要反正切运算，如果没有大量计算资源很难精确实现。所以我们使用了一种无需计算中间$\theta(n)$相位（及其令人讨厌的反正切）并可用于上式中的计算$∆\theta(n)$的方案。我们首先根据以下定义使用连续时间变量来得出$∆\theta(n)$的算法：

变量	定义
$i(t)$	同相信号
$q(t)$	正交信号
$θ(t)$	瞬时相位
$∆θ(t)$	$θ(t)$的时间导数

首先，我们令$r(t)=\frac{q(t)}{i(t)}$是我们要为其计算正切导数的信号。演算恒等式$tan^{-1}[r(t)]$的时间导数为:

$$∆θ(t)=\frac{d(tan^{-1}[r(t)])}{dt}=\frac{1}{1+r^2(t)}\frac{d[r(t)]}{dt}$$

因为$\frac{d[r(t)]}{dt}=\frac{d[\frac{q(t)}{i(t)}]}{dt}$，所以我们将微积分恒等式写做：

$$\frac{d[r(t)]}{dt}=\frac{d[\frac{q(t)}{i(t)}]}{dt}=\frac{i(t)\frac{d[q(t)]}{dt}-q(t)\frac{d[i(t)]}{dt}}{i^2(t)}$$

代入前式继而有：

$$∆θ(t)=\frac{1}{1+r^2(t)}\frac{i(t)\frac{d[q(t)]}{dt}-q(t)\frac{d[i(t)]}{dt}}{i^2(t)}$$

将$r(t)$替换，得：

$$∆θ(t)=\frac{1}{1+[\frac{q(t)}{i(t)}]^2}\frac{i(t)\frac{d[q(t)]}{dt}-q(t)\frac{d[i(t)]}{dt}}{i^2(t)}$$

接下来，我们将等式中第一个分数的分母展开与第二个分数分母相乘,然后将t替换为我们的离散时间变量n，化简得出最终结果为:

$$∆θ(n)=\frac{i(n)\frac{d[q(n)]}{dn}-q(n)\frac{d[i(n)]}{dn}}{i^2(n)+q^2(n)}$$

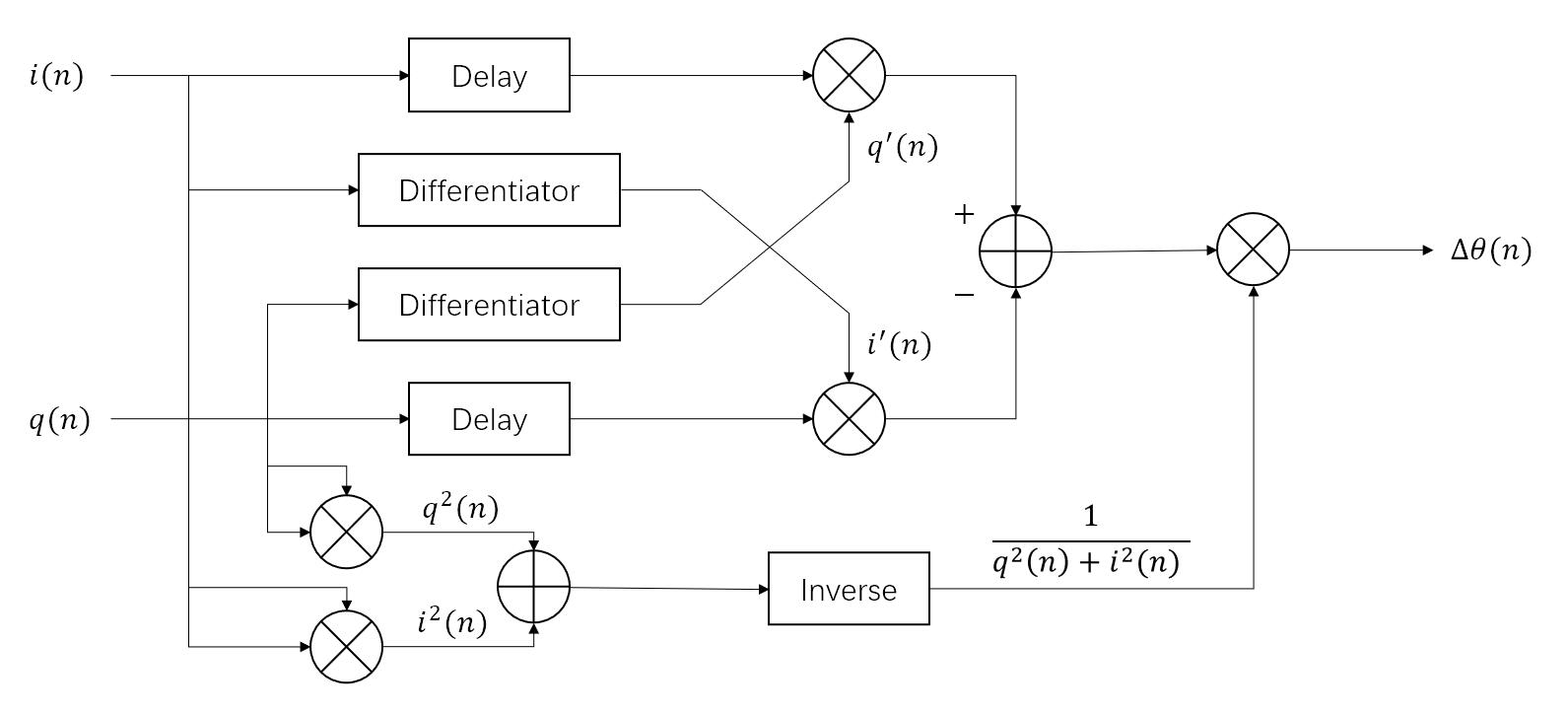
微分器是抽头延迟线FIR微分滤波器，具有奇数个抽头。当微分器是系数为1,0,–1的FIR滤波器时，得到了有效的结果。

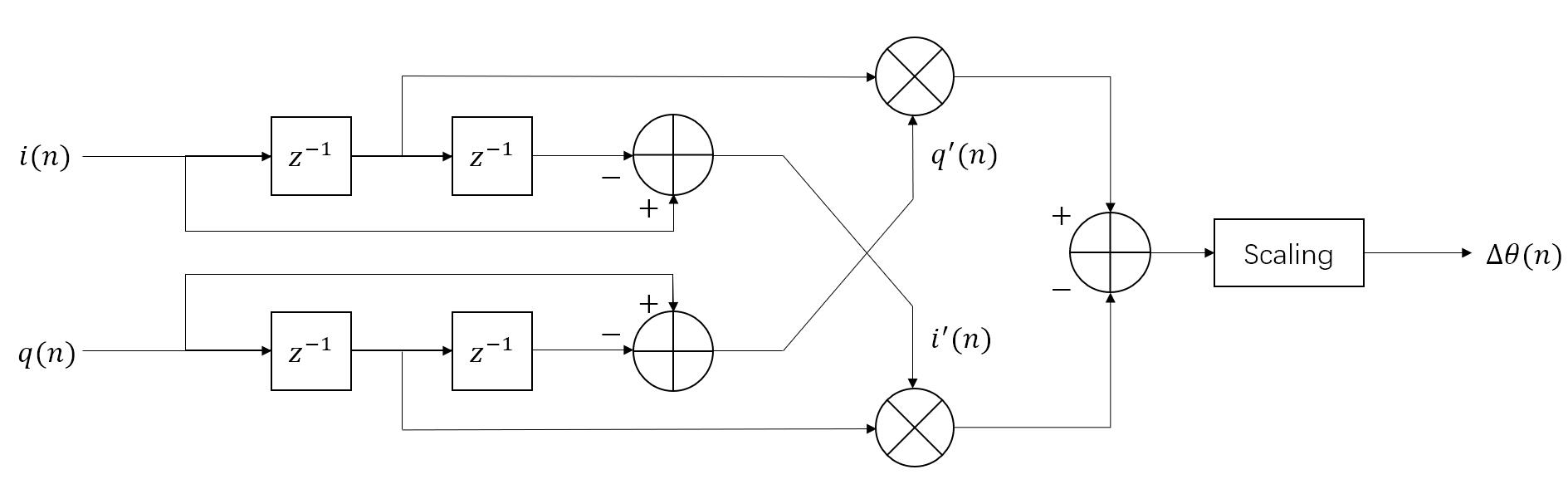
如果$i(n)+ jq(n)$信号纯粹是FM信号且受严格限制，使得$i^2(n)+q^2(n)=Const$（在硬件RTL中为常数1），则等式中的分母计算无需执行。在这种情况下，使用1,0,–1系数微分器，将FM解调器简化为图bz中的方法即可，其中比例运算直接与常数的倒数相乘。

参考文献: Richard G. Lyons, Understanding Digital Signal Processing[M], April 2004.